La inteligencia artificial (IA) también se equivoca, pero las matemáticas “no fallan”

La “no generalización de la IA” significa que un modelo solo es bueno con los datos específicos con los que fue entrenado y que no puede aplicar su conocimiento con datos que nunca ha visto, lo que no es del todo útil cuando se requiere medir el avance de un cáncer o hacer una lectura de resonancias magnéticas cerebrales para detectar tumores, escenario que exigen confiabilidad, es decir que el modelo sirva tanto con datos nuevos como con aquellos que fue entrenado.

“Cuando el modelo se entrena demasiado deja de comprender y memoriza hasta el ruido o los detalles irrelevantes de los datos, lo que lo hace incapaz de lograr buenos resultados cuando se necesitan información diferente con la que fue entrenado. Esto es un problema, ya que se espera que las máquinas aprendan y no memoricen”.

Así lo explica la ingeniera electrónica Manuela Viviana Chacón Chamorro, magíster en Ciencias - Matemática Aplicada de la Universidad Nacional de Colombia (UNAL) Sede Manizales, quien investigó un tipo especial de modelo de IA llamado “red neuronal residual”, arquitectura usada para tareas de clasificación.

El objetivo del aprendizaje en este contexto es encontrar los ajustes internos de la red o “pesos” a través de datos disponibles. A medida que se le presentan más datos, la red ajusta su configuración interna para clasificar de manera similar la información dada, sin embargo, a veces pueden surgir problemas de sobreajuste.

Para resolver esta dificultad se suelen probar muchos modelos y observar cuáles funcionan mejor con datos nuevos; en la investigación desarrollada se adoptó un enfoque diferente. “Analizamos las propiedades matemáticas del modelo y desarrollamos una solución pensada desde la teoría”, anota la magíster.

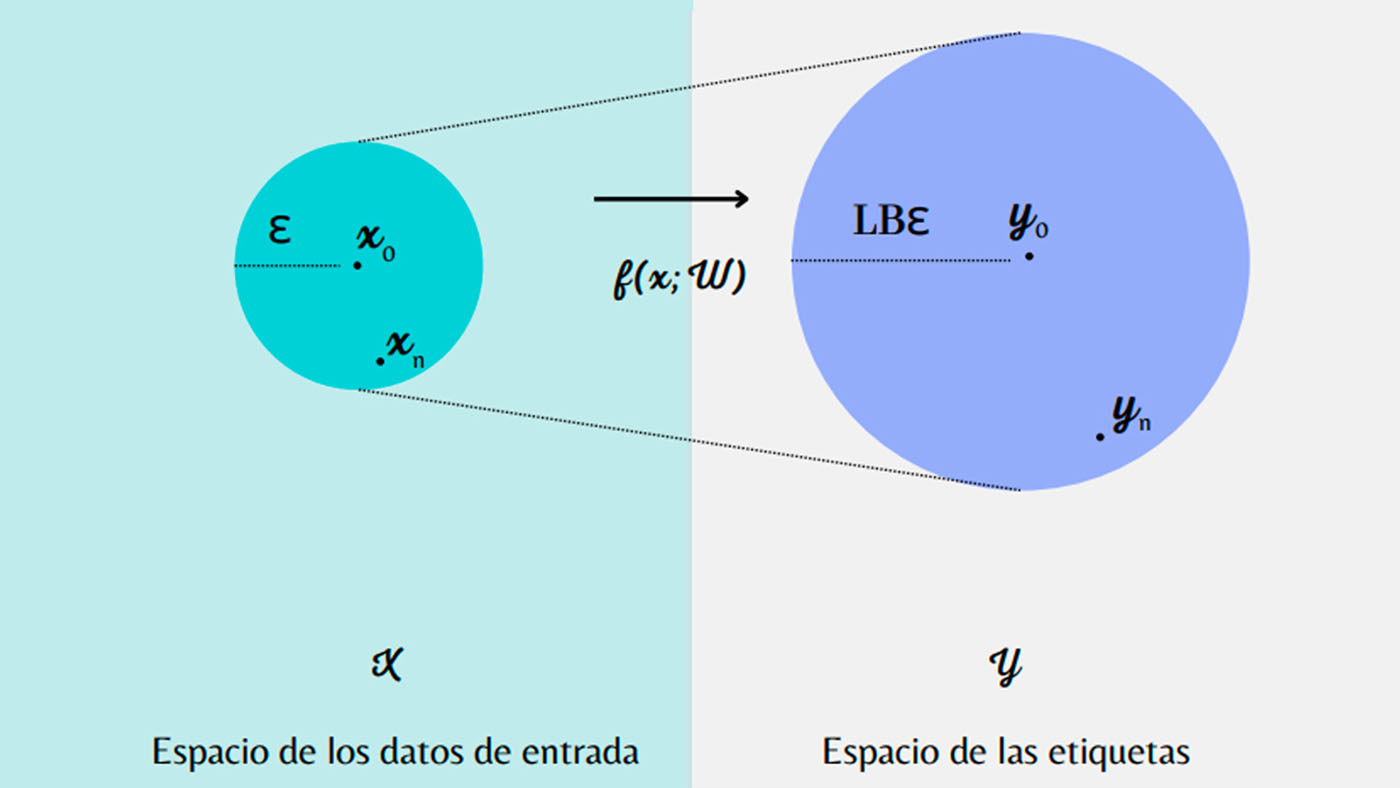
Para ello se consideraron las redes neuronales como reglas matemáticas (funciones) que, por ejemplo, convierten imágenes en números que representan su categoría. “Queríamos que la red tuviera una propiedad específica de las funciones matemáticas llamada ‘continuidad de Lipschitz’, lo cual significa que, en el ejemplo de la clasificación de imágenes, aquellas similares deberían tener resultados similares y que las diferencias entre resultados no deberían ser demasiado grandes cuando las entradas son parecidas”.

Después de realizar el aporte teórico se validaron los resultados en 4 experimentos: (i) clasificación de imágenes con datos de dígitos escritos a mano, (ii) clasificación de imágenes de prendas de vestir, (iii) clasificación de algunas bases de datos estándar, y (iv) datos sintéticos con configuración geométrica especial.

Las imágenes correspondían a: MNIST Digits, es decir números, y MNIST Fashion, prendas de ropa; las bases de datos: Flor Iris, características de flores, Wine Dataset, tipos de vino, y Cáncer de Mama de Wisconsin.

“También creamos conjuntos de datos sintéticos para evaluar propiedades geométricas, como patrones de espirales y rollos entrelazados. Comparando los modelos sin ningún método de control de sobreajuste, con enfoques clásicos y con nuestro algoritmo, observamos que nuestro método logra reducir el sobreajuste, aunque con una pequeña pérdida de precisión”.

“Este proceso irrumpe con el aprendizaje de máquinas convencional, al analizar desde adentro, con matemáticas, cómo se comporta la IA, aportando desde un entorno teórico experimental, con resultados óptimos para aplicarlo en un operativo, como una industria, un hospital, una base de datos industrial o empresarial, entre otros”, menciona la investigadora.

Esta propuesta en el campo de las matemáticas aplicadas y los sistemas computacionales se desarrolló con la dirección y asesoría del profesor Juan Carlos Riaño Rojas y de Fernando Gallego Restrepo, destacados expertos en matemáticas, además del apoyo y respaldo del grupo Computational Applications de la UNAL Sede Manizales.

Todos los algoritmos que se desarrollaron como parte de este proyecto están disponibles de forma gratuita en el repositorio: https://github.com/mavivi95/overfittingLipschitzBound